Research

My research interests lie at the interface between physics and biology. By applying physical methods and approaches to living systems we are able to test how far the physical approach can take us in understanding these complex systems. My research focuses on two distinct topics: neural processes involved in vision and tissue mechanics in early embryonic development. I have also used elastomechanical and statistical-mechanical models to understand aggregates of lipid vesicles and the structure of assemblies of animal cells.   

    A mechanical model of epithelial invagination

   

    Epithelial folding is a common morphological process in the development of animals. With the role of mechanics in morphogenesis becoming increasingly appreciated, we focused on the mechanics of a tubular epithelium resembling the early fruit fly embryo. We propose a two-dimensional mechanical model that relies only on the tension of the cell cortex and successfully reproduces epithelial folding that is observed in fruit fly embryos during gastrulation [Hocevar Brezavscek et al. Biophys. J. 103 (5), 1069 (2012)]. We also extended the model to describe folding of a periodic flat two-dimensional epithelium [Krajnc et al. Soft Matter 9, 8368 (2013)].

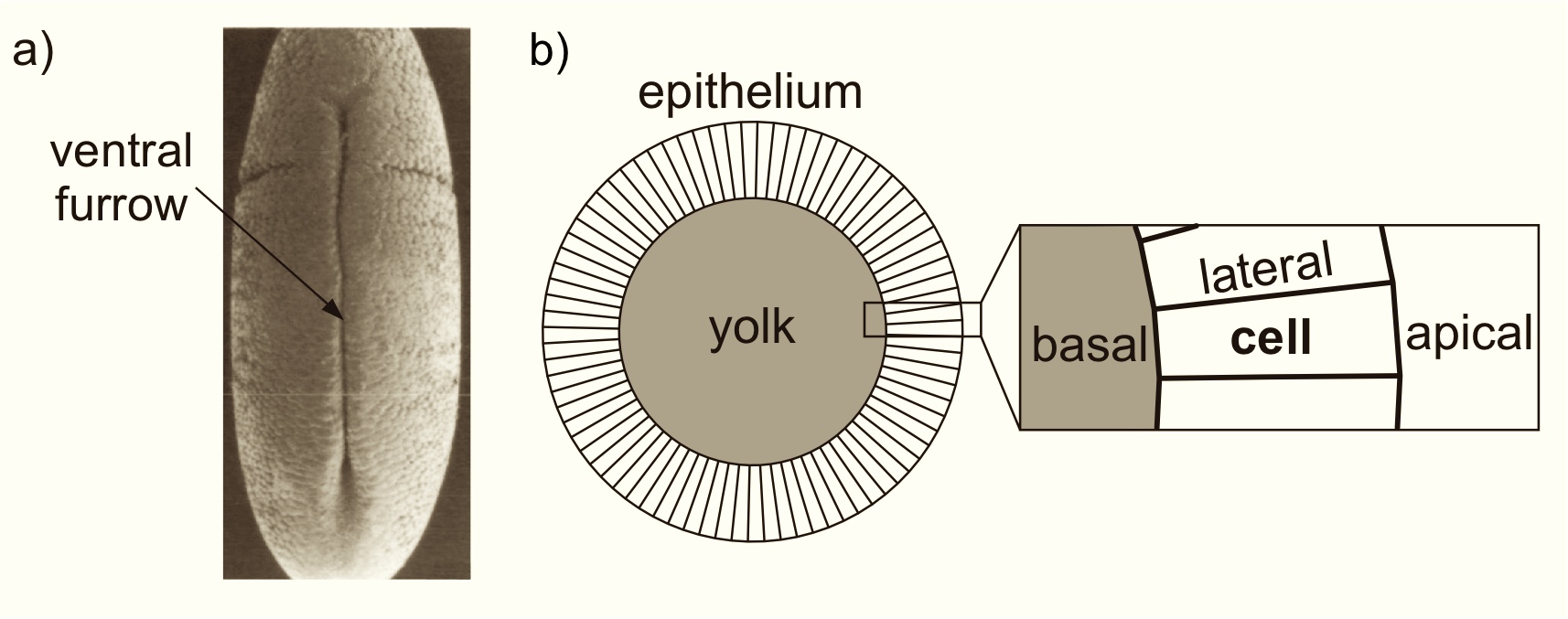
(a) Electron micrograph of the ventral side of a fruit fly embryo

showing a furrow. (b) The model embryo tissue cross section consists

of a ring of N quadrilateral cells

   

   

   

    Polygonal tilings in simple animal tissues (SEE POSTER)

   

    One of the projects of my research has been understanding simple biological tissues such as planar epithelia, in which, when observed from the top, cells resemble polygons that tile the plane.

SEM of mucosal epithelium in rat small intestine (image

courtesy of Dr. Roger Wagner, University of Delaware)

with a model tiling resulting from simulation placed on top.

In an attempt to unveil the mechanisms that control these natural tilings, we proposed a maximal entropy statistical-mechanical model. The experimental data from fruit fly tissues were found to be in good agreement with our simulations where the structure of the system is controlled by a single, purely geometric parameter.

This parameter, called reduced area a, measures the roundedness of polygons. It is defined as

                                              a = 4 Pi A / L2

where A is polygon area and L2 is polygon perimeter squared. Reduced area thus ranges from 0, when a polygon is a line, to 1, corresponding to a circle. However, in a planar tiling the maximal reduced area possible is smaller than 1 due to the constraint that polygons must tile the plane without pores or overlaps.

   The structure of the simulated monodisperse maximal entropy tiling controlled by the reduced area a is encoded in the frequencies of polygon classes. For values of a larger than 0.865 there are only hexagons present in the tiling, whereas for smaller values of a, other polygon classes exist as well [Hocevar and Ziherl, Phys. Rev. E 80, 011904 (2009)].

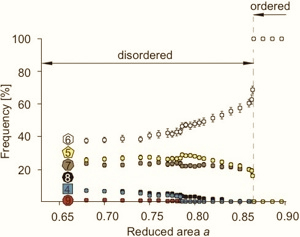
Frequencies of polygon classes as a function of reduced area a.

The order transition takes place at a=0.865.

    Universality of structure of living and inanimate planar tilings     (SEE POSTER)

   

   The fact that experimental data from biological tissues agreed well with our purely geometrical model led us to believe that the geometric constraint demanding that polygonal cells must tile the plane prevails over other mechanisms that mold a tissue. In an attempt to test this, we analyzed various other planar tilings seen in biological tissues as well as in geological formations, supermagnetic froths and tabletop experiments. Our results imply that there is a universal geometric mechanism that controls the structure of these tilings [Hocevar et al. EPJE 33, 369 (2010)].

   

   

    Geometry of bulk lipid vesicle aggregates (SEE POSTER)

   

   I also explored models of bulk tissues. Here cells of identical volume and area are modeled as polyhedral sticky lipid vesicles. In our model, each vesicle is assigned an elastic and an adhesion energy, and it turns out that the shapes of cells are governed by their total edge length minimization. In fact, this is an interesting mathematical problem, which is yet to be solved: how to partition space into identical cells such that their total edge length is minimal. We tested various space-filling polyhedra and the optimal cell shapes we obtained agree well with the available experimental data [Hocevar and Ziherl, Phys. Rev. E 83, 041917 (2011)].